「高齢者選挙権自主返納制度」を提案します.
この記事は移転しました。約2秒後に新記事へ移動します。移動しない場合はココをクリックしてください。
どうも,ざるご(@zalgo3)です.
最も平和的に高齢者から選挙権をはく奪できる制度「高齢者選挙権自主返納制度」を提案します.
65歳以上の高齢者を対象に,選挙権を自主返納すれば,自治体から様々な特典サービスを受けられるようにする制度を導入してはどうでしょうか?
【未来ある若者の意見を政治に反映するために高齢者から選挙権をはく奪すべき】という意見をよく耳にしますが,制度を変えるためにも選挙が必要.若者だけの力でこれを実現することは困難です.
高齢者にもメリットのあるこの制度であれば,高齢者の協力も得られる可能性があります.
続きを読む【2019年4月】LINE Payの20%還元+Amazonギフト券・Suicaチャージで錬金術する方法
この記事は移転しました。約2秒後に新記事へ移動します。移動しない場合はココをクリックしてください。

LINE Payの20%還元という激ヤバキャンペーンがまたも開催されている.
AmazonやSuicaへのチャージも対象
このキャンペーンのやばいところが,Amazonギフト券やSuicaへのチャージでも20%還元がもらえること.

最大10000円まで還元されるとのことなので,とりあえずAmazonに50000円ぶち込んでおけばそのまま10000円が手に入るというわけだ.まさに錬金術.
注意
注意が必要なのが次の二点
- 初期状態では5000円還元まで.10000円還元を受けるにはLINE Payアプリを期間中に一度利用する必要あり.
- 20%還元は会員ランク(マイカラー)が最高かつコード支払いのとき.キャンペーンで還元されるのは15%のみ.
一点目,LINE Payアプリを一度でも利用すれば還元の上限が二倍になる.コンビニで適当な商品でも買っておくべし!*1
二点目,実はこのキャンペーンは15%還元しか提供しない.しかし,還元率を20%まで上げられるからくりが2つある.
一つはコード支払い.LINE Payの決済方法はいくつかあるが,そのうちの「コード支払い」というものを選択すると3%の還元率が上乗せされる.
もう一つは「マイカラー制度」.LINE Payには,前月の支払い額に応じてポイント還元率が変わるマイカラーという仕組みがある.

このマイカラーが最高ランクのグリーンのとき,更に2%ポイント還元となり,15+3+2=20%還元が受けられる.
デフォルトの会員ランクはホワイト(0.5%)なので,最低限保証される還元率は15+0.5=15.5%だ.
しかしどちらにせよ,このキャンペーンには参加するべき
しかしながら,Amazonギフト券チャージが対象となれば,そんなことはあまり関係ない.
20%還元なら50000円チャージすれば10000円がもらえるが,15.5%還元なら65000円チャージすれば10000円がもらえる.それだけの話である.
どちらにせよ,タダで10000円もらえるという事実に変わりはない.
Amazonギフト券の有効期限は10年である.10年でその金額が使い切れないということはまずないだろう.
Amazonギフト券のチャージは↓から.LINE PayカードはJCBのクレジットカード扱いなので,LINEアプリから見れるカード番号を入力すればよい.購入前にLINE Payに残高を追加しておくのを忘れずに.
なお,Prime会員やPrimeスチューデント会員であればamazonギフト券チャージの際に0.5%がamazonポイントとして還元される.
無料体験期間中もこちらのポイント還元の対象となるので,この機会に是非登録しよう.
Prime会員登録→Amazon.co.jp: Amazon Prime
Prime Student会員登録→
Amazon.co.jp: Prime Student - 学生のためのお得なプログラム
紹介は以上となります.LINE Payはここ3ヶ月連続くらいで20%還元キャンペーンを打っているので,ぜひ今のうちに使い始めたほうがいいと思います!キャンペーン期間外でもコード支払いなら3.5%還元です!
Suicaチャージの方法は↓
LINE PayでSuicaにチャージする方法、キャンペーン等で効果的にLINE Pay還元を受ける1つの策 | アプリオ
20%還元キャンペーンの詳細は↓
よければ読者登録やTwitterのフォローよろしくお願いします。
*1:ファミリーマートやローソンなら100円引きなどのLINEクーポンが利用できる.
Chainerチュートリアルは初学者がディープラーニングをサクッと理解するのに超おすすめのサイト
この記事は移転しました。約2秒後に新記事へ移動します。移動しない場合はココをクリックしてください。
Preferred Networks (PFN)が公開したChainerチュートリアル,話題になっていたので読んでみましたがほんとにサクサク読めてわかりやすかったです.
日本語の文献なので英語ワカリマセンという方もぜひ読んでみましょう.
現時点で公開されてる「ディープラーニング入門」の章まで読むのに所要時間がだいたい3時間半でした.
高校数学の知識さえあれば,それ以外の前提知識が全くない人でも半日あれば余裕で読み切れるんじゃないかな?
ということで,以下に簡単に書評を記します.
教材の内容
Step 1 準備編
- はじめに
- Python入門
- 機械学習に使われる数学
- 微分の基礎
- 線形代数の基礎
- 確率・統計の基礎
まず,この6章で前提となるプログラミングや数学の知識を網羅しています.
2のPython入門では,変数の使い方や四則演算などの超基本的なことから解説されているので,プログラミング言語を全く触ったことのない人でも読み進められると思います.
しかし,必要なことだけがコンパクトに書かれているので,多少知識のある人が読んでも苦にはなりません.こういう教材だと基本的なことに紙面を割きすぎて読み手が疲れてしまうというのがありがちなのですが,そこがクリアされているのはお見事という感じです.
3から6では,数学的な基礎知識が解説されています.こちらも,x2の微分が2xであるというようなほんとにごく基礎的な部分から,最尤推定やベイズの事後確率などの統計的学習理論に欠かせない部分までコンパクトにまとまっていました.
Step 2 機械学習とデータ分析入門
- 単回帰分析と重回帰分析
- Numpy入門
- scikit-learn入門
- Cupy入門
- Pandas入門
- Matplotlib入門
この章では,機械学習・データ解析の基本的な例として,7で回帰分析をとりあげ,実際にPythonで回帰分析を行う様子を8-12で解説しています.
機械学習の便利なライブラリであるscikit-learnをはじめ,数値計算のnumpy,GPU計算のCupy,データフレームのPandas,可視化のMatplotlibの使い方がそれぞれコンパクトにまとまっています.
この章を読めば機械学習の基本的な流れは抑えられると思う.
Step 3 ディープラーニング入門
- ニューラルネットワークの基礎
- Chainerの基礎
- Chainerの応用
- トレーナーとエクステンション
この章を読めば,ディープラーニングが大体わかります.(多分)
まず13で,順伝播と誤差逆伝播法,確率的勾配降下法などの,ニューラルネットワーク(ディープラーニング)に使う数学的な理論が簡単に記されています.
そして14-16ではディープラーニングのフレームワークであるChainerを使った具体的な実装方法が記されています.単なる使い方だけでなく,簡潔にコードを書く方法や,ログの取り方など,必要な情報がもれなく抑えられています.
しかしながら,Chainerというフレームワークの扱いやすさも相まって,非常に説明が頭にすっと入ってくる印象でした.
注目ポイント
初学者向けだけど,ダラダラ無駄な情報を書いていない!
とにかくここに尽きます.
人間の集中力というのはそう長くは持ちません.分厚い教科書に飽きて挫折してしまった経験は誰しもあるでしょう.
しかし,この教材は本当に必要な情報のみを厳選して書いていて,集中力がなくなる前に読み切れてしまいます.
初学者にもある程度知っている人にもおすすめの教材です.
よければ読者登録やTwitterのフォローよろしくお願いします。
ブラックホール撮影にも使える「スパースモデリング」とは?【機械学習】
この記事は移転しました。約2秒後に新記事へ移動します。移動しない場合はココをクリックしてください。
どうもざるご(@zalgo3)です.
世界初のブラックホール撮影の成功例が出たようです.
ブラックホールの撮影に成功 世界初 一般相対性理論を証明 - 毎日新聞
今回のブラックホール撮影は,スパースモデリングという機械学習技術を取り入れたことによる貢献が大きいようです.
天文学に計算機科学の知識が取り入れられて,大きな成果が出たというのは,驚くべきことだと思います.
今回はそんな大成功を巻き起こした「スパースモデリング」について解説していきます.
スパースモデリングとは
スパースモデリングとは,誤解を恐れずにざっくりいうと解けない連立一次方程式を無理やり解くための仕組みです.
次のような連立一次方程式を考えます.
この方程式は,が逆行列を持つときに解くことができて,
となります.では,が逆行列を持たないときはどうなるでしょうか?
高校や大学1年生で習った数学では,そういう連立方程式は解けないと習ったと思います.「不能」とか「不定」とかいうやつですね.
ただ,実用上の観点からいうと,せっかく式があるのにハイ解けませんで片付けてしまうのは少々もったいないところがあるんですよね.
そこで登場するのがスパースモデリングです.スパースモデリングでは,以下の2つを仮定することによって解なしの連立一次方程式でも無理やり解を求めてしまいます.
が完全に満たされなくてもよく,
と近似的に成り立てばよいものとする.
がスパース(疎)であるとする.
スパース(疎)というのは人によってはあまり馴染みのない表現かもしれません.
スパースというのは,疎という字からも連想されるように,データ(0以外の要素)がまばらであることをいいます.
ベクトルがスパースであるというのは,
の要素のほとんどが0で,0以外の要素がちょっとだけある,つまり
のようなベクトルであるということです.
実世界で観測されるデータには,スパースなものが多いということが知られています.
今回の研究で扱われた宇宙の観測データも,スパースなデータの1つです.
広大な宇宙は、ほとんど真っ暗な世界です。この中の限られた部分だけが天体として観測されるわけで、そうした意味でスパース性を仮定することは妥当だといえるでしょう.
では具体的にこれをどう解くか,というところを順を追って解説していきます.まず1から.
なるべくが
に近づくような
を手に入れたいわけです.そこで,次の関数を最小化することを考えます.
という記号は見慣れない人もいるかも知れませんが,高校で習うベクトルの絶対値
と同じです.つまり,上の問題の意味は,
の各成分の二乗和(二乗誤差)を最小化するという意味になります.
二乗和は必ず0以上となるので,この関数を最小化すれば0に近い値が得られるはずです.したがって,となるような
が得られるという理屈になります.
この方法を最小二乗法 (Least Squares Method)といいます.
しかし,これだけではがスパースになってくれるとは限りません.そこでさっきの関数の代わりに次の関数を考えます.
は適当な正の定数を表します.
というのは,の非ゼロ要素の個数を表す記号です(L0ノルムという).たとえば
のとき,
となります.
最小二乗法と違って,二乗誤差と一緒に非ゼロ要素の個数を最小化することになるので,非ゼロ要素の数が少ないスパースな解が得られます.
しかし,「非ゼロ要素の数」というのは連続的に変化せず,数学的に結構扱いづらい性質を持っています.そこでこれと似たような問題として,
の最小化を考えることがあります.
は,
の各成分の絶対値の総和を表します(L1ノルムという).
この問題も,解がスパースになるということがよく知られています.
さっきのL0ノルムと違って,L1ノルムは連続で扱いやすいため,こちらの問題が実用上はよく扱われます.
この問題を,LASSO (Least Absolute Shrinkage and Selection Operator)といいます.
さて,ここまでざっくりとしたアイデアを説明してきましたが,次はこのアイデアをブラックホール観測にどう活かしたのか?ということについて説明していきます.
ブラックホールとスパースモデリング
アインシュタインの相対性理論や,重力波の観測などの実験結果から,ブラックホールが存在することはほぼ確実とされています.
そこで近年では,ブラックホールが作り出す影(ブラックホールシャドウ)を撮影することで,ブラックホールの存在を立証しようという計画が進められてきました.
ブラックホール観測を成功させるための秘訣は,望遠鏡の空間分解能をあげることにあります.
「空間分解能」というのは,近接した2点をきちんと2点として認識できる能力,という意味です.
たとえば道路に家が2軒並んでいるような状況を考えましょう.
近所から見ると,「家が2軒あるな」ということはすぐにわかります.しかし,これを遠く離れた宇宙から見るとどうでしょうか?
おそらく人間の目では家が2軒あることを認識するのは不可能でしょう.では,望遠鏡で見るとどうでしょうか?
宇宙から撮影された衛星写真を見ると,家が2軒あることくらいは余裕で識別することができます.
この二つの違いを生じさせるのが空間分解能です.望遠鏡は,人間の目に比べて非常に高い空間分解能を持っています.
しかしそんな天体望遠鏡の空間分解能でも,ブラックホールを観測するには全く歯が立ちません.
ブラックホールとブラックホールの距離は,約1光年と言われています.一方,ブラックホールが存在する可能性のある銀河系で,地球から最も近いものでも,239万光年離れていると言われています.
スケールがでかすぎてよくわかりませんが,239km先にある1cm間隔のパチンコ玉を識別できるかと聞かれれば,その無理ゲーさが理解できると思います.
しかし,この無理ゲーを解決してこそ科学者です.そこで使われた解決策が,電波干渉計,そしてスパースモデリングです.
まず電波干渉計について.これは2つ以上の電波望遠鏡を連動させて,波の干渉を用いて空間分解能を向上させる技術です.
「波の干渉」といったら,高校物理を履修していた人は一度は聞いたことがあると思います.ヤングの干渉実験とかが有名なやつですね.
光は波の性質を持っているので,干渉が起こります.電波干渉計のアイデアは,2つの望遠鏡で観測された波が干渉したときの時間差を測定することで,波がどちらの方向から来たかを割り出すというところにあります.
この技術によって,空間分解能は飛躍的に上がります.
しかし,ブラックホールの観測にはこれだけじゃまだ足りないのです.ブラックホール恐るべし.
そこで近年になって注目されてきたのが,スパースモデリングです.
ブラックホール観測にスパースモデリングをどう用いるか,ぼくも完全に理解しているわけではないですが,ざっくりと書きます.
まず,電波干渉計で観測されたデータというのは,実際の天体画像
に,観測行列(フーリエ変換)
をかけてやったものと考えられます.つまり,
です.
目標は,天体画像を,なるべく高解像度で復元してやることとなります.(空間分解能をあげるため)
基本的に望遠鏡の数はそんなにたくさんは使えないので,の逆行列を求めて方程式をそのまま解くという方法は使えません.
そこで生きるのがさっきのスパースモデリングです.
次の関数を最小化して(LASSO),天体画像を復元してやります.
この方法により,実際に研究チームが復元した画像がこちらです*1.
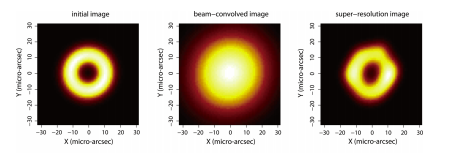
この研究からさらに様々な改良が重ねられ,今回の報道が合ったような大発見につながったようです.
まとめ
5000文字を超える長文記事になってしまいましたが,今回の大発見のすばらしさ,そしてスパースモデリングの魅力について少しでも伝えられていたら幸いです.
まだぼくもスパースモデリングについては勉強中の身なので,間違っている点等あったら申し訳ないです.ぜひコメントとかで教えてくださると嬉しいです.
また,この記事でスパースモデリングに興味を持った人向けに,入門の教科書のリンクをいくつか貼っておきます.一緒に勉強しよう!
スパース推定法による統計モデリング (統計学One Point)
スパースモデリングで用いられるモデルがざっくりと書いてある本.
細かい証明等はほとんどないが,イメージを掴むのにおすすめ.
スパースモデリング- 基礎から動的システムへの応用
基礎から応用までしっかり書かれている本.
ソースコード例も載っているので,実際にプログラムを実装しながら学びたい人にはおすすめ.

- 作者:永原 正章
- 出版社/メーカー: コロナ社
- 発売日: 2017/10/06
- メディア: 単行本
スパース性に基づく機械学習 (機械学習プロフェッショナルシリーズ)
数学的な背景までスパースモデリングをガッツリ知りたい人向け.
ぼくのように証明がないと発狂してしまう人類はこちらを.

スパース性に基づく機械学習 (機械学習プロフェッショナルシリーズ)
- 作者:冨岡 亮太
- 出版社/メーカー: 講談社
- 発売日: 2015/12/19
- メディア: 単行本(ソフトカバー)
宣伝
学術系の知識とかをおもしろおかしく解説するYouTubeチャンネルをやってます.
↓の動画は「安定マッチング」というグラフ理論の問題について解説した動画です.
まだ動画数は少ないですが,今後機械学習やスパースモデリングについても動画を出していこうと思っているのでよければチャンネル登録よろしくお願いします!
【京大式】数学的に最も正しい彼氏彼女の作り方を解説【安定結婚問題】
よければ読者登録やTwitterのフォローよろしくお願いします。
*1:本間ら「スパースモデリング天文学 ― ブラックホール撮像から時間変動減少まで」,科学研究費補助金新学術領域研究「スパースモデリングの深化と高次元データ駆動科学の創成」最終成果報告会 (2017/12/18-20)
「社会勉強のためのアルバイト」ほど無駄なものはない
この記事は移転しました。約2秒後に新記事へ移動します。移動しない場合はココをクリックしてください。
「バイトは無駄か」論争の際に,バイト擁護派から最もよく発せられる言葉が以下である.
バイトは社会勉強になる(からやったほうがよい)
だが断言しよう,「社会勉強のためのバイト」はバイトの中でもとびきりクソである.クソというかもはやウンチであると言えよう.
「社会勉強」という言葉はふわっとしすぎている
なるほど確かに役に立つアルバイトはある.
通訳になりたい人が通訳バイトで実務経験を積むというのは非常に理にかなっている.
エンジニアを目指す人がスタートアップでプログラムを使った業務をやってみるというのも確かに面白いだろう.
研究者を志す人がリサーチ・アシスタントとして研究室に雇われてみるというのは必ずいい経験になると思う.
しかし,これらのバイトにおいて,目的はすべて具体的だ.
このような,「本当に将来につながるバイト」をする人が,社会勉強などという言葉を使うだろうか?いや,絶対に使わない.(反語)
本当に「社会勉強」をしたいなら,「こういうスキルを学びたい」「こういう知識を付けたい」と,もっと具体的な言葉で自分の目的を説明できるはずだ.
なのに,「社会勉強」なんてふわっとした言葉を使っている人は,その時点で「逃げ」の姿勢が丸見えなのである.
具体的な目標があれば,「それを達成できたか否か」が客観的にわかる.
しかし,抽象的な言葉しか使わなければ,達成度をきちんと判定することはできない.
ふわっとした言葉を使って,結局できたのかどうかもなあなあにしてるクソみたいな奴らが,「バイトは社会勉強」とか言ってるのだ.こんな奴らの真似をする必要は一切ない.
だいいち,「バイトは社会経験だ」とか言ってしまう人は,バイトをしなかった時間という意識が欠落している.
バイトをせずに勉強した時間,バイトをせずに友だちと遊んだ時間,バイトをせずに家でダラダラ寝た時間,すべてが社会経験だ.
そりゃバイトから得るいい経験もたまにはあるかもしれない.
しかし,いろんな選択肢がある中から,最も自分にとって有意義な時間を選択していくことが重要なのに,「バイトから得るものが1mmでもあるか」だけを語るというのは,もう圧倒的に間違えている.
家でダラダラ寝る経験から得るものだって,たまにはあるに決まっている.
バイトから得られるものなんて,他の経験に比べればクソほどどうでもいい.学生ならバイトよりも勉強しろ.就業体験がしたいならインターンにいけ.暇なら友達と遊べ.バイトなんて,まじでやる意味ない.まじでクソミソみたいなものだ.
とりあえず,こんなところで今日の記事は終わります.ありがとうございました.ところで近況報告なのですが,最近アルバイト始めました.
よければ読者登録やTwitterのフォローよろしくお願いします。
渡辺真由子の博士号剥奪で「博士号の信用が下がった」とか勘弁してくれ
この記事は移転しました。約2秒後に新記事へ移動します。移動しない場合はココをクリックしてください。
ジャーナリストの渡辺真由子氏が,慶応大学から博士号を取り消されたことが話題になっている.
https://www.yomiuri.co.jp/national/20190321-OYT1T50183/www.yomiuri.co.jp

